An executable operational semantics for Python

The following article gives a taste of the work that I’ve done for my master’s thesis at the University of Utrecht under the supervision of Andres Löh. If you are interested, feel free to have a look at the source files.

Introduction

Programming languages are often specified only in an informal manner; in the available documentation, the language behaviour is described by examples and text. Only the implementation, a compiler or interpreter, describes the exact semantics of constructs.

Python is no different. It is described by an informal manual and a number of implementations. Notably the original implementation CPython and PyPy, an implementation of Python in Python. No systematic, formal descriptions of its semantics are available.

We developed a formal semantics for a comprehensive subset of Python called minpy. The semantics are described in literate Haskell, which are compiled to an interpreter as well as a formal specification.

Rewriting an abstract machine

The operational semantics are defined by state transitions of an abstract machine. A machine state consist of a heap Θ, an environment stack Γ, a control stack S, and an instruction ι. State transitions are defined by rewrite rules that transform the machine state. These rewrite rules have the following shape.

The heap represents the memory of the abstract machine. It is a mapping of addresses to values. Many different kinds of values are stored on the heap, for example integers, strings, lists and objects.

Even the environment is partly stored on the heap. The environment Γ consists of a stack of addresses, which correspond with the scoping blocks that have been entered. The addresses point to mappings on the heap, which in turn map variables to addresses.

The control stack is a stack of continuation frames, i.e., frames that indicate what to do next. One of the traditional functions of a control stack (also known as call stack) is to store the return pointer of a function call that is being executed.

The instruction is the abstract equivalent of a program counter. The instruction can be a piece of a program, such as an expression, statement, or a complete block. But, for example, when an expression has been evaluated it can also hold the resulting address.

Executing an assignment

To show what the rewrite rules look like we will have a look at the semantics of variable assignments. Starting with the execution of a variable assignment statement x = e; as instruction, a heap Θ, an environment Γ and a stack S.

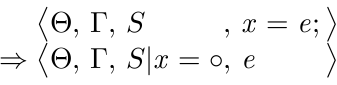
The state is rewritten to a new state that is virtually the same, except that a stack frame x = o is pushed onto the control stack and the expression e is the new instruction. The circle o in the new stack frame indicates that the expression which place it took, will be evaluated.

Once the expression has been evaluated, we end up with a state that has an address instruction a, a stack the assignment frame on top, an environment stack with an address γ₁ on top.

The address γ₁ on top of the environment stack points to the variables bound in the current scope. In the new state, the mapping that contains the bindings is changed to include the new assignment. The environment stack however, remains unchanged. The top stack frame is removed and the result of the assignment statement is None, or rather an address pointing to None.

The changes to the heap are not very intuitive, so let us be more precise: the existing environment mapping bound at γ₁ is overwritten with the old mapping Θ(γ₁) that itself has been extended with the mapping [x → a]. The notation of Θ(γ₁) represents the lookup of γ₁ on the heap Θ. The circled addition operator extends the mapping on its left hand side with the mapping on its right hand side. If the both sides of the circled addition operator have a mapping of the same variable or address, the right hand side takes precedence.

Literate programming

The semantics of minpy are described in literate Haskell, a syntax extension of Haskell that allows us to mix Haskell and LaTeX code in the same file. The Haskell compiler GHC will, when confronted with a literate Haskell file, simply ignore all the Latex code. Latex however, is not natively aware of the literate Haskell code, but can be instructed to include the Haskell code verbatim in the document.

To exploit the advantages of LaTeX typesetting, we preprocessed the literate Haskell sources with lhs2TeX. This tool transforms Haskell source code into a nicely formatted LaTeX equation. It handles horizontal alignment across multiple lines of code and allows us to customize the transformation through simple macros.

In order to hide all traces of Haskell from the formatted rewrite rules, we have pushed lhs2TeX to its limits. To achieve the current results we introduced an additional preprocessing stage, implemented by a simple Perl script. Furthermore, we had to accept certain restrictions on the Haskell vocabulary and adhere to a number of coding conventions. For example, every state has to be on a single line to get proper alignment. Some rules do not even fit on a 30″ monitor.

The resulting source code is nevertheless quite readable, especially when compared to any equivalent LaTeX code. For instance, the above rule for variable binding is defined by the following code.

rewrite  (State  ( heap                                              )  ( envs :|: env_1 )  ( stack :|: AssFrame x )  ( BwResult a      )) =
         (state  ( heap <+> [env_1 |-> get heap env_1 <+> [x |-> a]] )  ( envs :|: env_1 )  ( stack                )  ( BwResult a_None ))

Note that, while compiling the document requires several steps, GHC can still compile the source code in a single step. This allows us to experiment with the semantics, while ignoring the presentation.

The interpreter

The sources of the thesis and some supporting code that implements a parser, pretty printer, and an interactive interpreter, can be compiled by the Haskell compiler GHC to produce an interpreter. Like the interpreter of CPython, this interpreter has both a command-line modus and the ability to interpret files.

The following example shows a session of the interpreter in its command-line modus. First, we declare the factorial function in a single function definition statement. The statement is immediately executed if parsing succeeds. Next, we call the factorial function without an argument, which results in a TypeError exception. Finally we call it with a correct argument and exit the interpreter.

gideon@gideon-desktop:~$ minpy
>>> def fac(x) :
...     if x <= 0 :
...         return 1
...     else :
...         return fac(x-1) * x
...
>>> fac()
TypeError
>>> fac(4)
24
>>> exiting minpy

All this will be more than familiar to a Python programmer, except for the rather meager error message. The minpy interpreter can also print a trace of the abstract machine revealing any changes after every rewrite step. This has proven to be very useful when debugging the semantic rules.

The interpreter, and by proxy the semantics, was systematically tested by a test suite written in pure Python, or actually, minpy. Executing the suite with CPython results in only one failed test, as it is the reference for our semantics. Our interpreter still fails for 13 tests.

Scope of the semantics

As mentioned in the introduction, minpy includes a significant number of Python constructs. Functions, generators, objects and classes, operators, exceptions, if, while, for, exec, and import statements are supported, although most only in a simplified form. Class declarations, for instance, must always specify the bases of the class.

Currently, minpy does not have any garbage collection, support for concurrency or foreign functions. It should also be noted that, while minpy does support multiple inheritance, the implementation of metaclasses is still incomplete.